Page 22 - sst-2022b
P. 22
Η αλληλεπίδραση των δύο σολιτονίων αρχικά φαίνεται
ότι είναι μια γραμμική διαδικασία (σχήμα 2), το οποίο
όμως δεν ισχύει (σχήμα 4): υπάρχει μια αλλαγή φάσης
που είναι το χαρακτηριστικό αυτού του τύπου
αλληλεπίδρασης. Παρουσιάζουμε επίσης τη λύση που
διαχωρίζει αυτούς τους δύο τύπους λύσεων (σχήμα 3).
Αυτό γίνεται πιο ευκρινές με την αναπαράσταση της
λύσης τη χρονική στιγμή t=0, και την παράμετρο
= − να παίρνει τιμές στο διάστημα (√2, 2), όπου
για = √3 , παρατηρούμε αυτή την ποιοτική
διαφοροποίηση στη μορφή της λύσης.
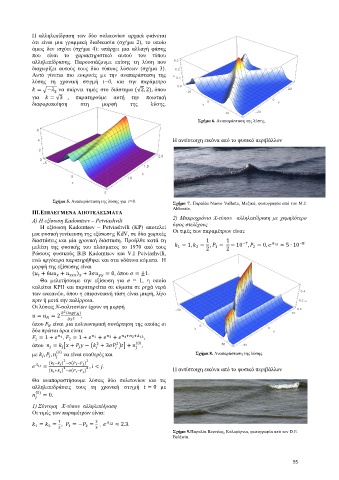
Σχήμα 6. Αναπαράσταση της λύσης.
Η αντίστοιχη εικόνα από το φυσικό περιβάλλον
Σχήμα 5. Αναπαράσταση της λύσης για t=0. Σχήμα 7. Παραλία Nuevo Vallarta, Μεξικό, φωτογραφία από τον M.J.
Ablowitz.
III. ΕΠΙΛΕΓΜΕΝΑ ΑΠΟΤΕΛΕΣΜΑΤΑ
Α) Η εξίσωση Kadomtsev – Petviashvili 2) Μακροχρόνια Χ-τύπου αλληλεπίδραση με χαμηλότερο
Η εξίσωση Kadomtsev – Petviashvili (KP) αποτελεί ύψος στελέχους
μια φυσική γενίκευση της εξίσωσης KdV, σε δύο χωρικές Οι τιμές των παραμέτρων είναι:
διαστάσεις και μία χρονική διάσταση. Προήλθε κατά τη 1 1
μελέτη της φυσικής του πλάσματος το 1970 από τους = 1, = 2 , = − 10 , = 0, ≈ 5 ∙ 10
2
Ρώσους φυσικούς B.B Kadomtsev και V.I Petviashvili,
ενώ αργότερα παρατηρήθηκε και στα υδάτινα κύματα. Η
μορφή της εξίσωσης είναι
( + 6 + = 0, όπου = ±1.
) + 3
Θα μελετήσουμε την εξίσωση για σ = 1, η οποία
καλείται KPII και παρατηρείται σε κύματα σε ρηχά νερά
των ωκεανών, όπου η επιφανειακή τάση είναι μικρή, λίγο
πριν ή μετά την παλίρροια.
Οι λύσεις Ν-σολιτονίων έχουν τη μορφή
( )
= = 2 ,
όπου είναι μια πολυωνυμική συνάρτηση της οποίας οι
δύο πρώτοι όροι είναι:
= 1 + , = 1 + + + ,
όπου = + − + 3 + ( ) ,
( )
με , , να είναι σταθερές και Σχήμα 8. Αναπαράσταση της λύσης.
= , < .
Η αντίστοιχη εικόνα από το φυσικό περιβάλλον
Θα αναπαραστήσουμε λύσεις δύο σολιτονίων και τις
αλληλεπιδράσεις τους τη χρονική στιγμή = 0 με
( )
= 0.
1) Σύντομη Χ-τύπου αλληλεπίδραση
Οι τιμές των παραμέτρων είναι:
= = , = − = , ≈ 2.3.
Σχήμα 9.Παραλία Βενετίας, Καλιφόρνια, φωτογραφία από τον D.E.
Baldwin.
55