Page 23 - sst-2022b

Β)Η μονοδιάστατη μη γραμμική εξίσωση Schrödinger
Ελάχιστες παρατηρήσεις υπάρχουν διαθέσιμες για την
κατανόηση των ακραίων κυμάτων στην επιφάνεια του
ωκεανού και η διαδικασία είναι αρκετά σύνθετη. Επειδή
τα ακραία κύματα μπορούν να δημιουργηθούν σε οπτικά
συστήματα είναι δυνατή η παραγωγή και η μελέτη
οπτικών ακραίων κυμάτων στα εργαστήρια. Η
μονοδιάστατη μη γραμμική εξίσωση Schrödinger (NLS),
με μη μηδενικές συνοριακές συνθήκες, μπορεί να
μοντελοποιήσει τη δυναμική τέτοιων κυμάτων στον
ωκεανό καθώς και τη διάδοση παλμών στις οπτικές ίνες.
Θα μελετήσουμε δύο σολιτονικές λύσεις της
μονοδιάστατης μη γραμμικής εξίσωσης Schrödinger

+ + 2| | = 0.

( )
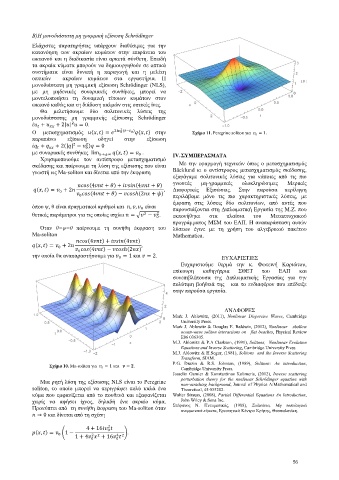
Ο μετασχηματισμός ( , ) = ( , ) στην Σχήμα 11. Peregrine soliton για = 1.
παραπάνω εξίσωση οδηγεί στην εξίσωση

+ + 2(| | − ) = 0

με συνοριακές συνθήκες lim →± ( , ) = . IV. ΣΥΜΠΕΡΑΣΜΑΤΑ

Χρησιμοποιούμε τον αντίστροφο μετασχηματισμό
σκέδασης και παίρνουμε τη λύση της εξίσωσης που είναι Με την εφαρμογή τεχνικών όπως ο μετασχηματισμός
γνωστή ως Ma-soliton και δίνεται από την έκφραση Bäcklund κι ο αντίστροφος μετασχηματισμός σκέδασης,
εξαγάγαμε σολιτονικές λύσεις για κάποιες από τις πιο
γνωστές μη-γραμμικές ολοκληρώσιμες Μερικές
(4 + ) + (4 + )
( , ) = + 2 , Διαφορικές Εξισώσεις. Στην παρούσα περίληψη

(4 + ) − ℎ(2 + ) περιλάβαμε μόνο τις πιο χαρακτηριστικές λύσεις, με

έμφαση στις λύσεις δύο σολιτονίων, από αυτές που
όπου ψ, θ είναι πραγματικοί αριθμοί και , , είναι παρουσιάζονται στη Διπλωματική Εργασία της Μ.Ζ. που

θετικές παράμετροι για τις οποίες ισχύει = − . εκπονήθηκε στα πλαίσια του Μεταπτυχιακού

προγράμματος ΜΣΜ του ΕΑΠ. Η αναπαράσταση αυτών
Όταν θ=ψ=0 παίρνουμε τη συνήθη έκφραση του λύσεων έγινε με τη χρήση του αλγεβρικού πακέτου
Ma-soliton Mathematica.
(4 ) + (4 )
( , ) = + 2 ,

(4 ) − ℎ(2 )

την οποία θα αναπαραστήσουμε για = 1 και = 2. ΕΥΧΑΡΙΣΤΙΕΣ

Ευχαριστούμε θερμά την κ. Φωτεινή Καριώτου,
επίκουρη καθηγήτρια ΣΘΕΤ του ΕΑΠ και
συνεπιβλέπουσα της Διπλωματικής Εργασίας για την
πολύτιμη βοήθειά της και το ενδιαφέρον που επέδειξε
στην παρούσα εργασία.
ΑΝΑΦΟΡΕΣ
Mark J. Ablowitz, (2011), Nonlinear Dispersive Waves, Cambridge
University Press.
Mark J. Ablowitz & Douglas E. Baldwin, (2012), Nonlinear shallow
ocean-wave soliton interactions on flat beaches, Physical Review
E86 036305.
M.J. Ablowitz & P.A Clarkson, (1991), Solitons, Nonlinear Evolution
Equations and Inverse Scattering, Cambridge University Press.
M.J. Ablowitz & H.Segur, (1981), Solitons and the Inverse Scattering
Transform, SIAM.
Σχήμα 10. Ma-soliton για = 1 και = . P.G. Drazin & R.S. Johnson, (1989), Solitons: An introduction,
Cambridge University Press.
Josselin Garnier & Konstantinos Kalimeris, (2012), Inverse scattering
Μια ρητή λύση της εξίσωσης NLS είναι το Peregrine perturbation theory for the nonlinear Schrödinger equation with
soliton, το οποίο μπορεί να περιγράψει πολύ καλά ένα non-vanishing background, Journal of Physics A:Mathematical and
Theoretical, 45 035202.
κύμα που εμφανίζεται από το πουθενά και εξαφανίζεται Walter Strauss, (2008), Partial Differential Equations An Introduction,
χωρίς να αφήσει ίχνος, δηλαδή ένα ακραίο κύμα. John Wiley & Sons Inc.
Προκύπτει από τη συνήθη έκφραση του Ma-soliton όταν Στέφανος Ν. Πνευματικός, (1988), Σολιτόνια, Μη τοπολογικά
αναρμονικά κύματα, Ερευνητικό Κέντρο Κρήτης, Θεσσαλονίκη.
→ 0 και δίνεται από τη σχέση

4 + 16

( , ) = 1 − .

1 + 4 + 16

56